第 4 章非线性模型

想学会飞翔，就必须先学会站立、行走、奔跑、攀登和跳舞，没有人能直接飞翔。

—— 尼采

让我们继续沿着从线性模型到非线性模型的道路进行探索，先从线性模型的逐渐修改开始，一步一步接触到非线性模型的精髓。

4.1 logistic 回归

在统计学中，logistic 回归被用于预测分类变量的各种结果的概率。这个名字有一定的误导性，事实上 logistic 回归是一种分类技术，而不是回归。但这种分类的通过概率的估计得到的，因此使用术语“回归”。

logistic 回归大部分是由一个线性模型运行的，但 logistic 函数 (图 4-1) 被用来将线性预测器的输出转化为一个 $0\sim1$ 的值，这也可以解释为概率。

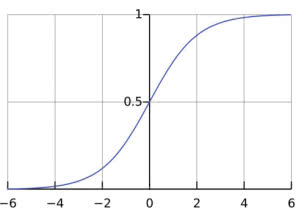
图 4-1 logistic 函数把输入值以平稳的方式转换为 0~1 的输出值

标准的 logistic 函数由下式定义：

P(t) = \frac{1}{1+e^{-t}} \tag{4-1}

其中 $e$ 是欧拉数。变量 $t$ 可以是时间，不过这里 $t$ 是线性模型的输出，回顾式 $\text{(3-2)}$ 有：

y = \frac{1}{1+e^{-(\boldsymbol{w}^\top\boldsymbol{x})}} \tag{4-2}

这里线性模型 $\boldsymbol{w}$ 也可以包括一个常数值 $w_0$ ，前提是在输入值列表中人为添加一个总是等于 1 的输入值 $x_0$ 。式 $\text{(4-2)}$ 可变化为：

\ln\frac{y}{1-y} = \boldsymbol{w}^\top\boldsymbol{x} \tag{4-3}

因为我们将输出值 $y$ 看作是正例的概率，所以 $1-y$ 是其反例的概率，两者的比值：

\frac{y}{1-y} \tag{4-4}

称为几率，反映了 $\boldsymbol{x}$ 作为正例的相对可能性。因此式 $\text{(4-2)}$ 实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率，因此 logistic 回归又被称为对数几率回归。

线性变换权重的最佳值是通过最大似然估计来确定的。给定数据集 $\{(\boldsymbol{x}_i,y_i)\}_{i=1}^l$ ，logistic 回归模型最大化对数似然：

\text{LogLikelihood}(\boldsymbol{w}) = \sum_{i=1}^l \ln p(y_i|\boldsymbol{x}_i;\boldsymbol{w}) \tag{4-5}

即令每个样本属于其真实标记的概率越大越好。令 $y_i$ 为所观察到的输出（1 或 0），对应输入为 $\boldsymbol{x}_i$ 。若正确分类为 1，则获得测量输出值 $y_i$ 的概率为 $p(y=1|\boldsymbol{x}_i)$ ；若正确分类标签为 0，则 $p(y=0|\boldsymbol{x}_i)=1-p(y=1|\boldsymbol{x}_i)$ 。于是式 $\text{(4-5)}$ 可以重写为：

\text{LogLikelihood}(\boldsymbol{w}) = \sum_{i=1}^l\{y_i\ln p(y=1|\boldsymbol{x}_i,\boldsymbol{w}) + (1-y_i)\ln(1-p(y=1|\boldsymbol{x}_i,\boldsymbol{w}))\} \tag{4-6}

似然率与系数（权重） $\boldsymbol{w}$ 的相关性已经非常明确了。

因为 logistic 回归的输出就是正例的概率，显然有：

\begin{align} p(y=1|\boldsymbol{x}_i,\boldsymbol{w}) &= \frac{1}{1+e^{-(\boldsymbol{w}^\top\boldsymbol{x})}} = \frac{e^{\boldsymbol{w}^\top\boldsymbol{x}}}{1+e^{\boldsymbol{w}^\top\boldsymbol{x}}} \\ p(y=0|\boldsymbol{x}_i,\boldsymbol{w}) &= \frac{1}{1+e^{\boldsymbol{w}^\top\boldsymbol{x}}} \end{align} \tag{4-7}

因此最大化式 $\text{(4-6)}$ 等价于最小化

L(\boldsymbol{w}) = \sum_{i=1}^l\Big(-y_i\boldsymbol{w}^\top\boldsymbol{x}_i + \ln(1+e^{\boldsymbol{w}^\top\boldsymbol{x}_i})\Big) \tag{4-8}

由于上述表达式中的非线性性，我们不可能找到使似然函数最大化的权重的解析表达式，而必须用迭代过程来代替，例如梯度下降法。

4.2 局部加权回归

本节中考虑的方法类似于最近邻值的输出的线性组合，但我们不会只关注 $K$ 个最近邻值而消除所有其他值的影响。这是一种平滑的变化：根据和被预测的实例之间的距离来逐渐减少实例对预测的影响，而不是选择一组 $K$ 个胜者。

局部加权回归是一种懒惰的基于存储的技术，这意味着所有点和评估值都被存储了，而只有查询特定的某点的时候才会基于请求建立特定的模型。

为了预测一个点 $\boldsymbol{q}$ （称为查询点）的评估结果，我们对训练点应用线性回归。为了确保在确定回归参数过程中的局部性（相近的点更相关），给每个样本点分配一个权重，这个权重会随着与查询点距离的增加而减小，我们用 $s_i$ 来表示。

加权后的最小二乘拟合的目标是最小化下面的加权误差（式 $\text{(3-3)}$ 中隐式地假设了每个点的权重是一样的）：

\text{error}(\boldsymbol{w};s_1,...,s_n) = \sum_{i=1}^l s_i(\boldsymbol{w}^\top\boldsymbol{x}_i-y_i)^2 \tag{4-9}

为了最小化式 $\text{(4-7)}$ ，可以令其关于 $\boldsymbol{w}$ 的梯度等于 0，得到如下解：

\boldsymbol{w}^* = (\boldsymbol{X}^\top\boldsymbol{S}^2\boldsymbol{X})^{-1}\boldsymbol{X}^\top\boldsymbol{S}^2\boldsymbol{y} \tag{4-10}

其中 $\boldsymbol{S} = \text{diag}(s_1,...,s_d)$ 。当所有权重相等时，式 $\text{(4-8)}$ 简化为式 $\text{(3-6)}$ 。

根据存储的样本到查询点的距离，可以使用以下函数来描述它们的重要性：

s_i = \exp\bigg(-\frac{\|\boldsymbol{x}_i-\boldsymbol{q}\|^2}{W_K}\bigg) \tag{4-11}

其中 $W_K$ 是度量“核宽度”的一个参数，即对远距离实例的灵敏度；当距离远大于 $W_K$ 时，重要性迅速衰减至 0。

4.3 用 LASSO 来缩小系数和选择输入值

考虑线性回归模型时，岭回归是一种通过二次方式来惩罚大系数，从而使得模型更稳定的方法，如式 $\text{(3-7)}$ 所示。

普通的最小二乘估计法通常偏差较小，但是方差较大。为了提高准确率，有时可以将一些系数缩小或者设置为零。通过这样做，我们牺牲一点偏差，以减少预测值的方差，从而可以提高整体的预测准确率。

特征子集选择和岭回归，这两个改进估计的标准技术仍然存在一些缺陷：子集选择提供了便于解释的模型，但由于它是一个离散过程，输入变量要么保留，要么删除，该模型的变化也可能是特别大的；岭回归是一种连续让系数缩小，从而使得模型更稳定的过程，然而它没有设置任何系数为零，所以无法得出一个易于解释的模型。

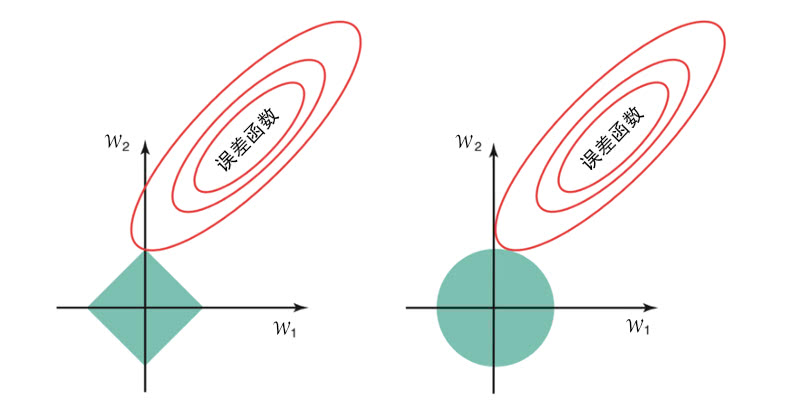
图 4-2 在 LASSO 中，最好的解决方法出现在二次误差函数等高线接触正方形处，有时会在正方形的角上，对应某些零系数。相反，岭回归的二次约束没有角来让等高线接触，因此权重中很少会产生零

最小绝对收缩和选择算符 LASSO 使得一些系数缩小而另一些设置为零，因此保持了子集选择和岭回归两种方法的优势。LASSO 使用权重绝对值的总和作为约束 $\|\boldsymbol{w}\|_1$ （参数向量的 $L_1$ 范数）。LASSO 在系数绝对值总和小于一个常数的约束下，使得残差平方和最小化。通过一个标准技巧，将带约束的优化问题通过拉格朗日乘数法转化为无约束的问题，这相当于将 $\lambda\|\boldsymbol{w}\|_1$ 加入无约束最小化的最小二乘：

\text{LASSOerror}(\boldsymbol{w};\lambda) = \sum_{i=1}^l(\boldsymbol{w}^\top\boldsymbol{x}_i-y_i)^2+\lambda\sum_{j=0}^d|w_j| \tag{4-12}

LASSO 和岭回归一个最主要的区别是，在岭回归中随着惩罚的增加，所有系数减小，但保持非零的状态，而 LASSO 随着惩罚的增加会导致更多的系数变为零。对应的权重为零的输入值就可以消除，从而导致模型使用较少的输入值（输入的稀疏化），因此更便于解释。换言之，作为模型构建过程的一部分，LASSO 是一种进行特征选择的嵌入式方法。

注意，式 $\text{(4-12)}$ 中 $\lambda\sum_{j=0}^d|w_j|$ ，当权重为零时不存在导数（偏导数从对应负值的 $-1$ 跳到对应正值的 $+1$ ），因此无法通过计算导数并令其等于零来求解。优化 LASSO 的问题可以通过引入带线性不等式约束的二次规划或更一般的凸优化方法来解决。 $\lambda$ 的最佳值可以通过交叉验证来获得。

拉格朗日乘数优化约束问题
LASSO 将带约束的优化问题转化为无约束的优化问题，并已被广泛应用。在数学优化中，拉格朗日乘数法是在带约束的前提下用来寻找函数局部最大值和最小值的方法。带约束问题是通过将各个约束乘以一个参数（一个拉格朗日乘数）转化为无约束的。